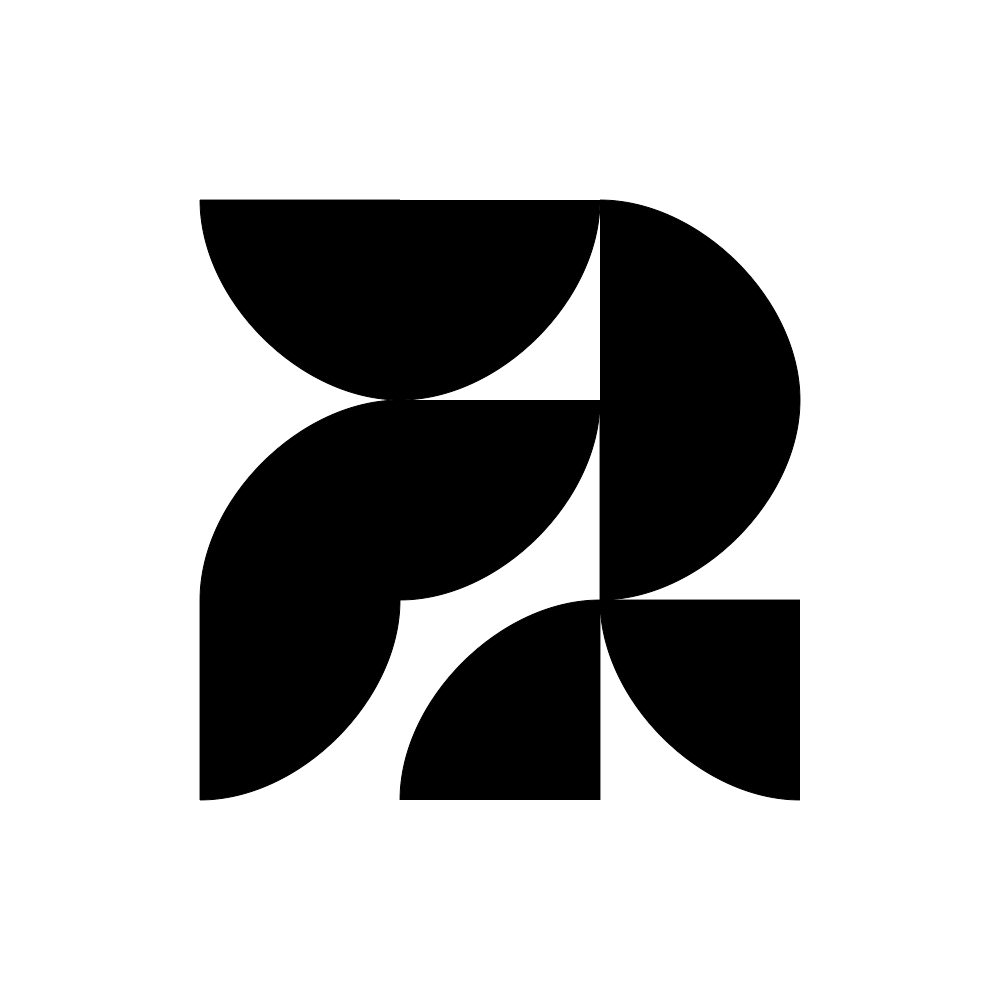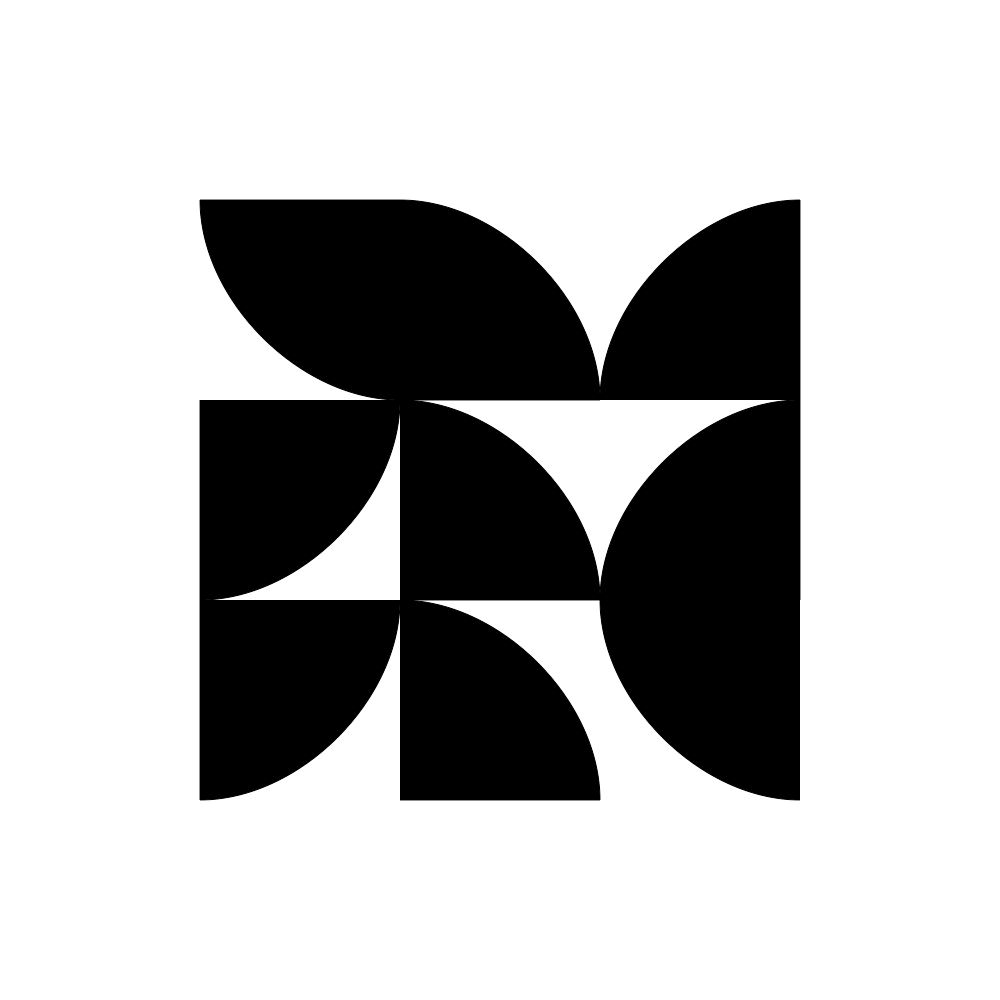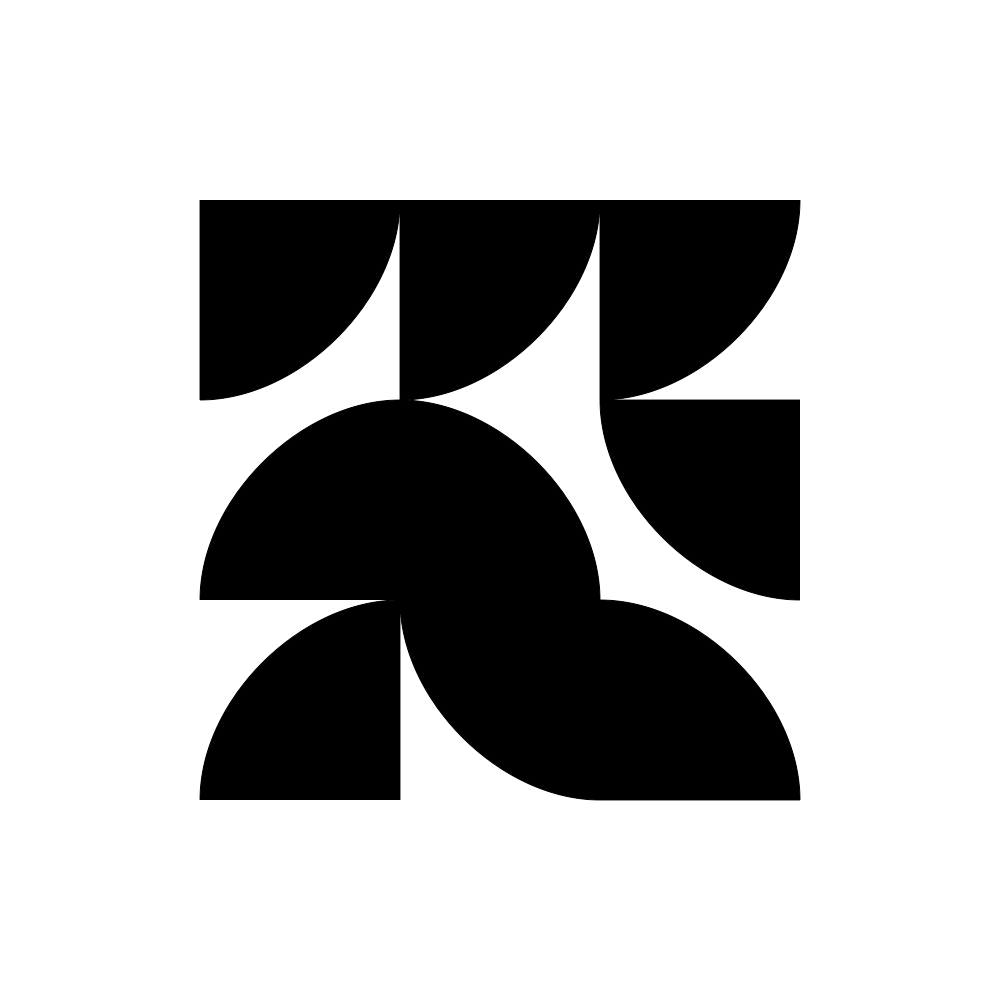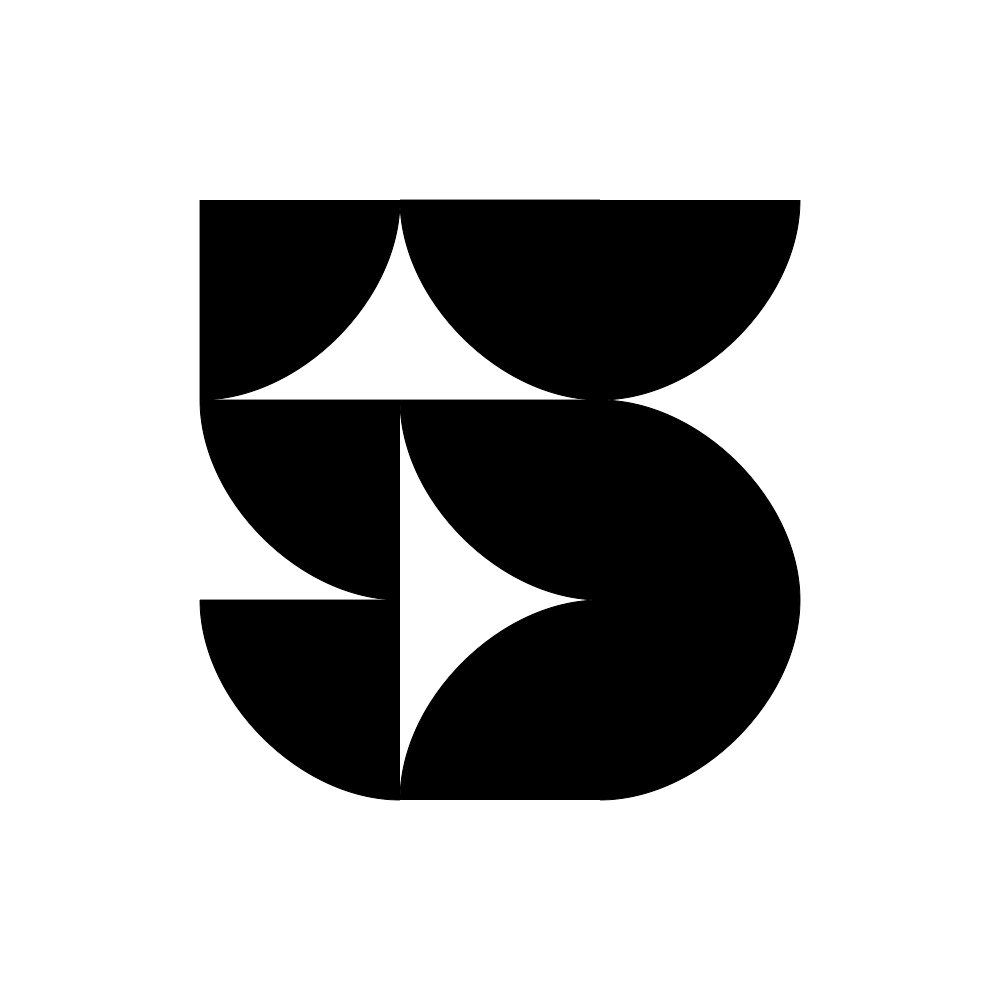


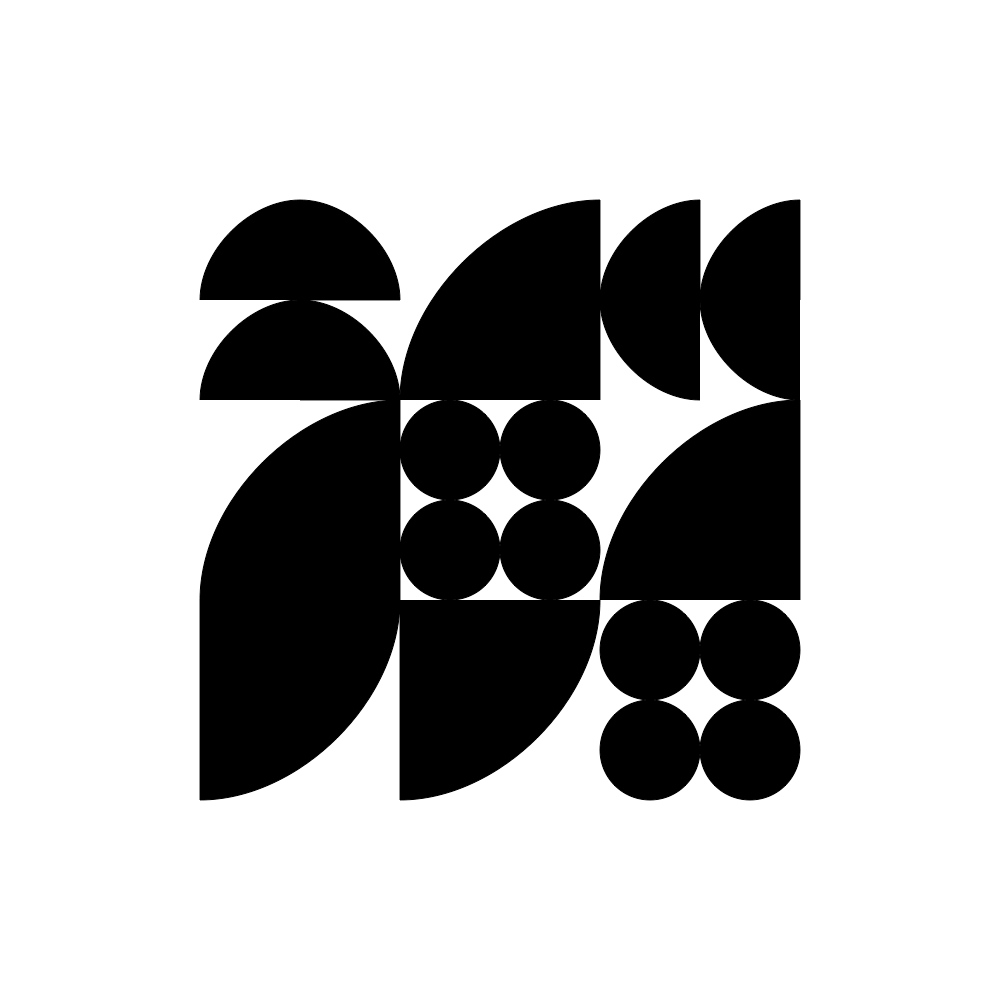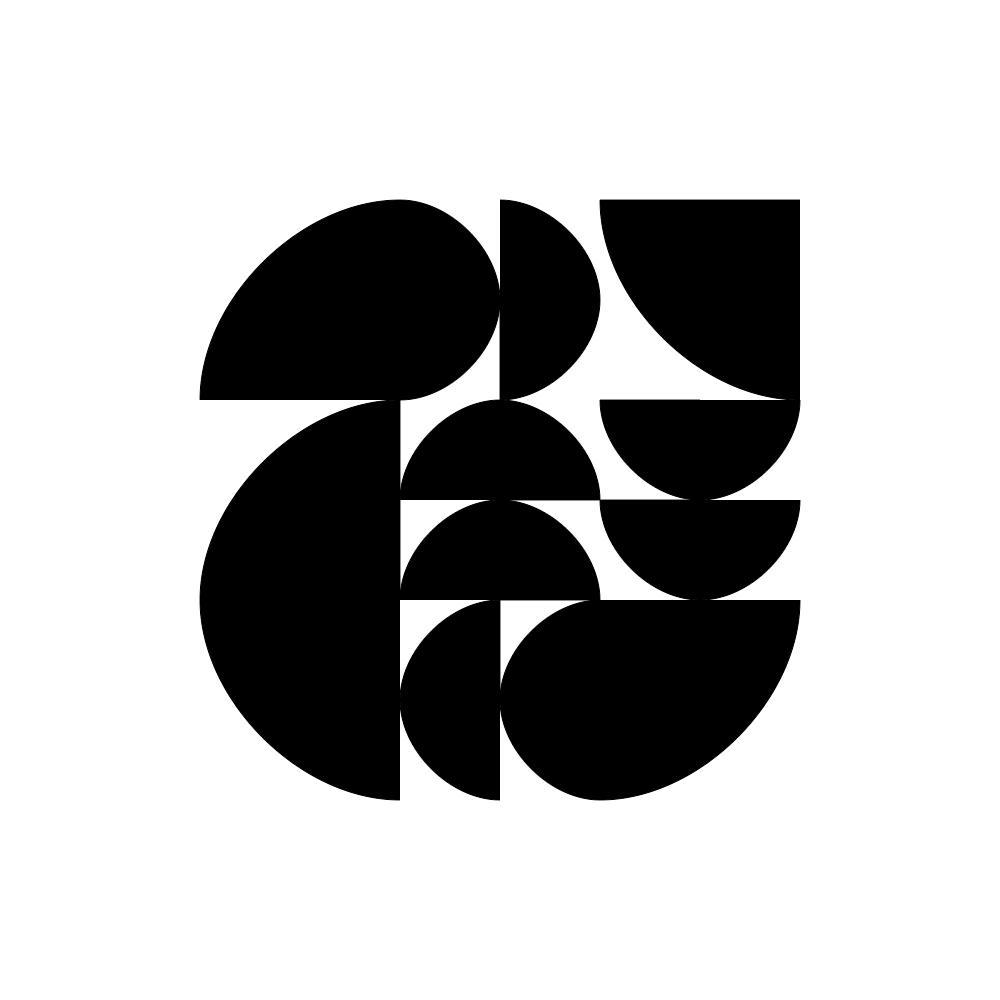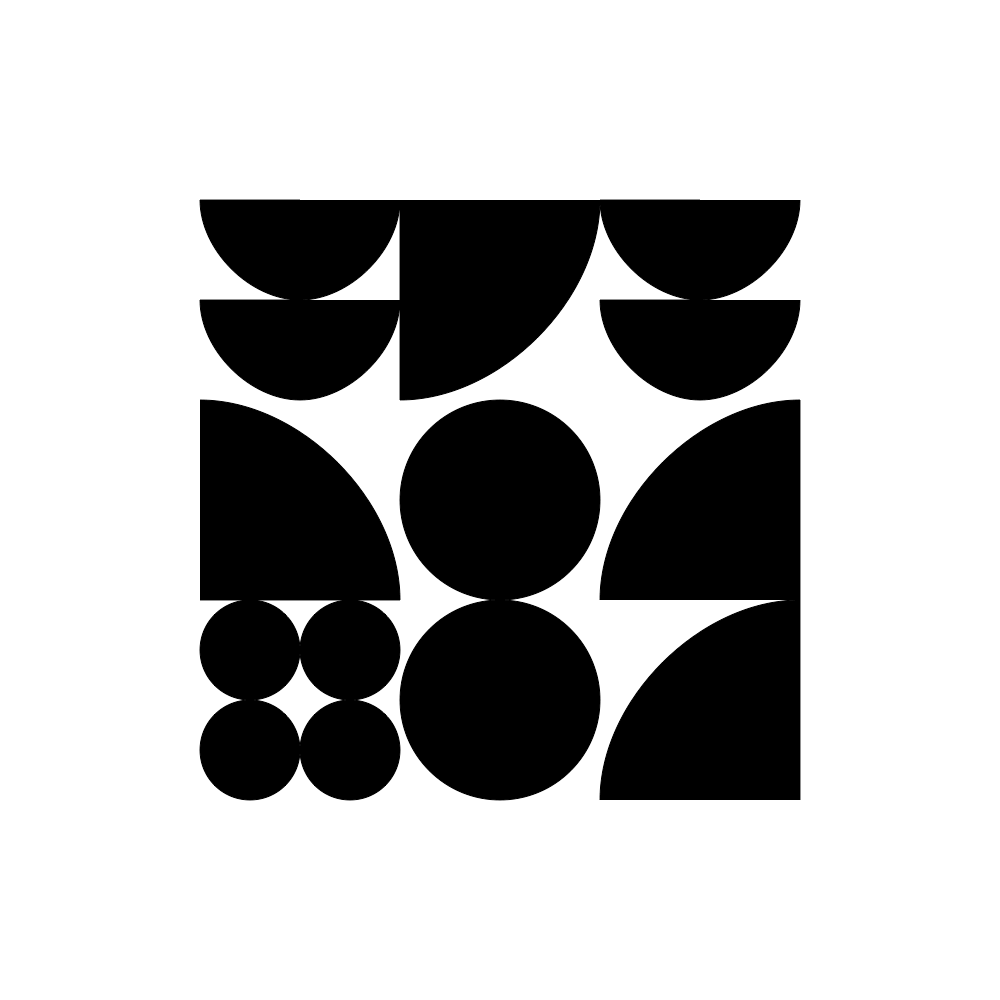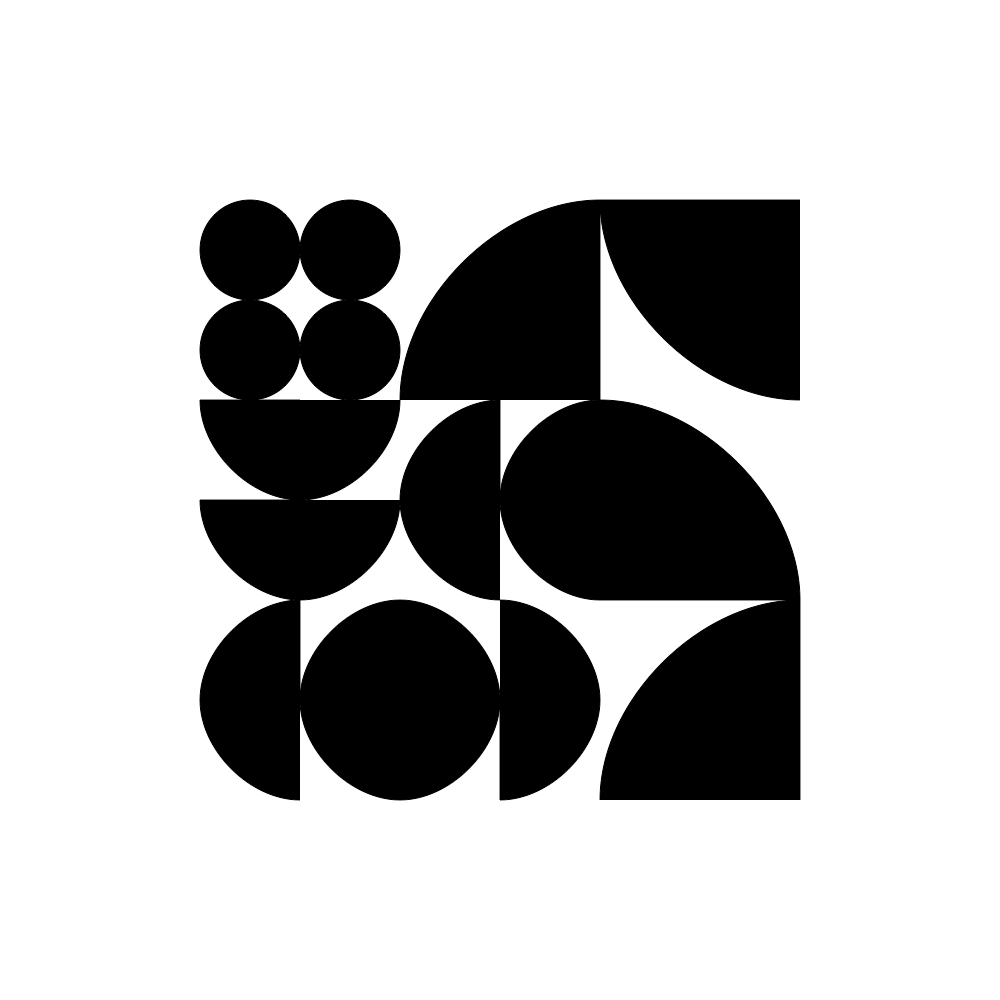
All Possible Arcs
python/drawbot
This series of gifs are exported from example scripts used to teach generative processes and variable design spaces. These were written in Python and executed by the opensource program for creative Python coding, DrawBot.
Students use iterative hand-coding on a variable coordinate grid to expose the mechanical processes behind how a computer draws visual form (type). Through a sequence of workshops and prompts, they then expand this to key programmatic concepts; like automation, randomization, looping & logic gates. The emphasis is on developing a process in which small variation can yield unexpected or generative surprise.
In this example script math and combinatorics demonstrate the complexity of a variable design space. Grids have a 2n rule if the option for any given cell is on/off (or black white) where n = number of cells in the design space... When there are more than two options for any given cell, then grids have a Kn rule where K = number of variants. This has a 3x3 grid which is 29 positions. There are up to 4 variants in the example scripts. So, 4 to the power of 29 = 2.8823038e+17 possible forms (a lot!) but the unique combinations are likely not this high.
Links to the annotated .py scripts are available below.
Students use iterative hand-coding on a variable coordinate grid to expose the mechanical processes behind how a computer draws visual form (type). Through a sequence of workshops and prompts, they then expand this to key programmatic concepts; like automation, randomization, looping & logic gates. The emphasis is on developing a process in which small variation can yield unexpected or generative surprise.
In this example script math and combinatorics demonstrate the complexity of a variable design space. Grids have a 2n rule if the option for any given cell is on/off (or black white) where n = number of cells in the design space... When there are more than two options for any given cell, then grids have a Kn rule where K = number of variants. This has a 3x3 grid which is 29 positions. There are up to 4 variants in the example scripts. So, 4 to the power of 29 = 2.8823038e+17 possible forms (a lot!) but the unique combinations are likely not this high.
Links to the annotated .py scripts are available below.

↑ allPossibleArcs.py example script : here.

↑ allPossibleHalfCircles.py example script : here.
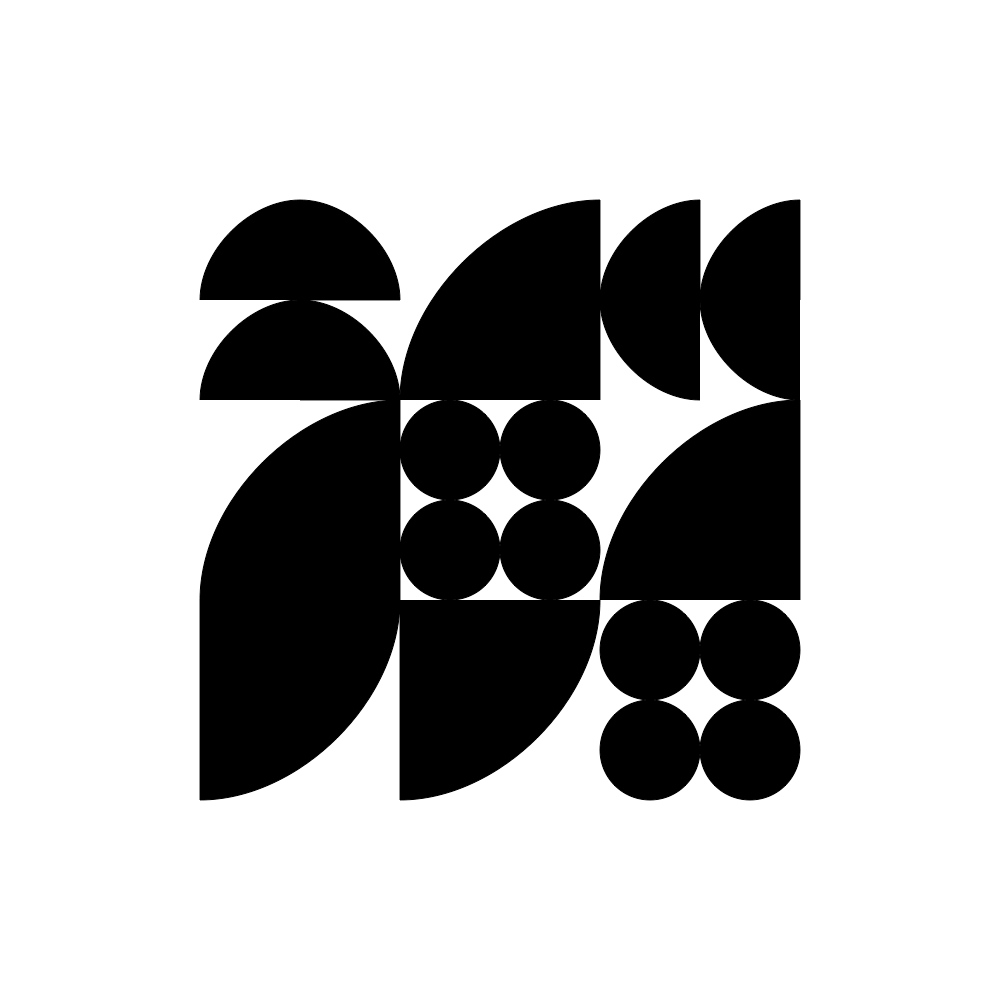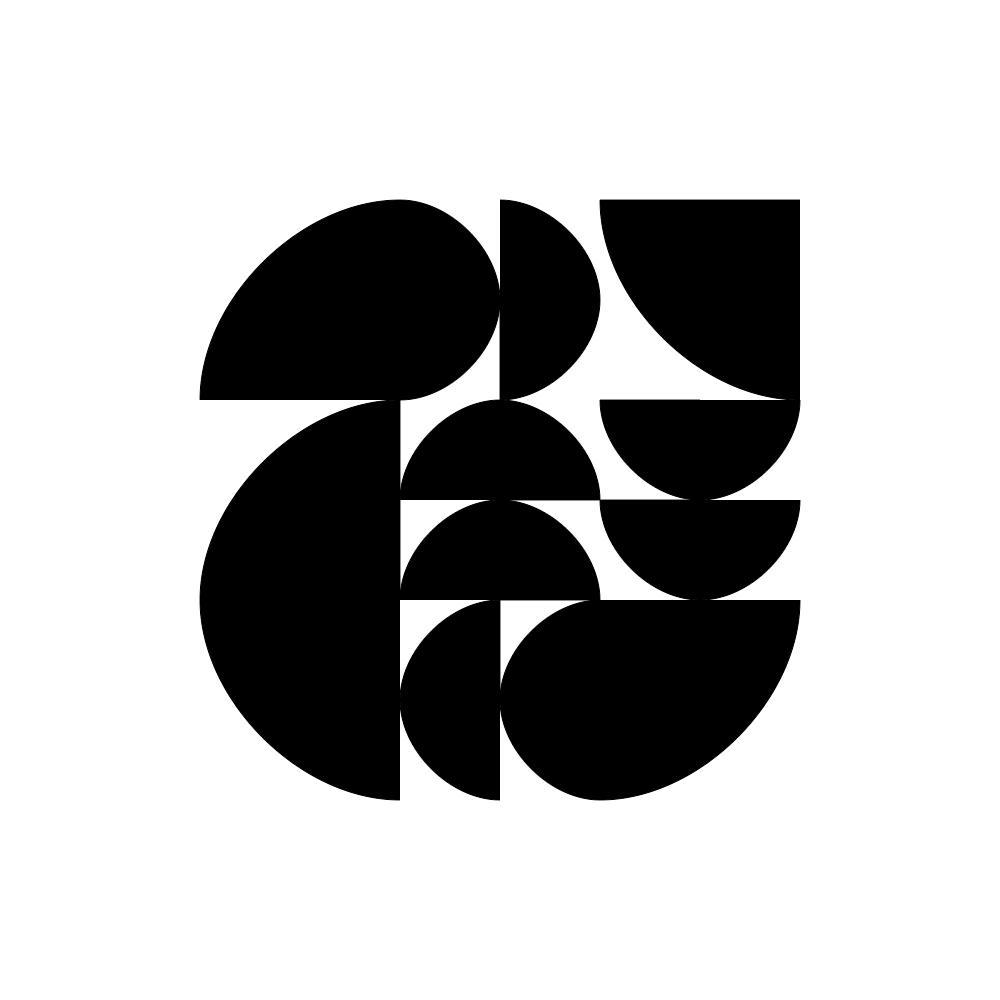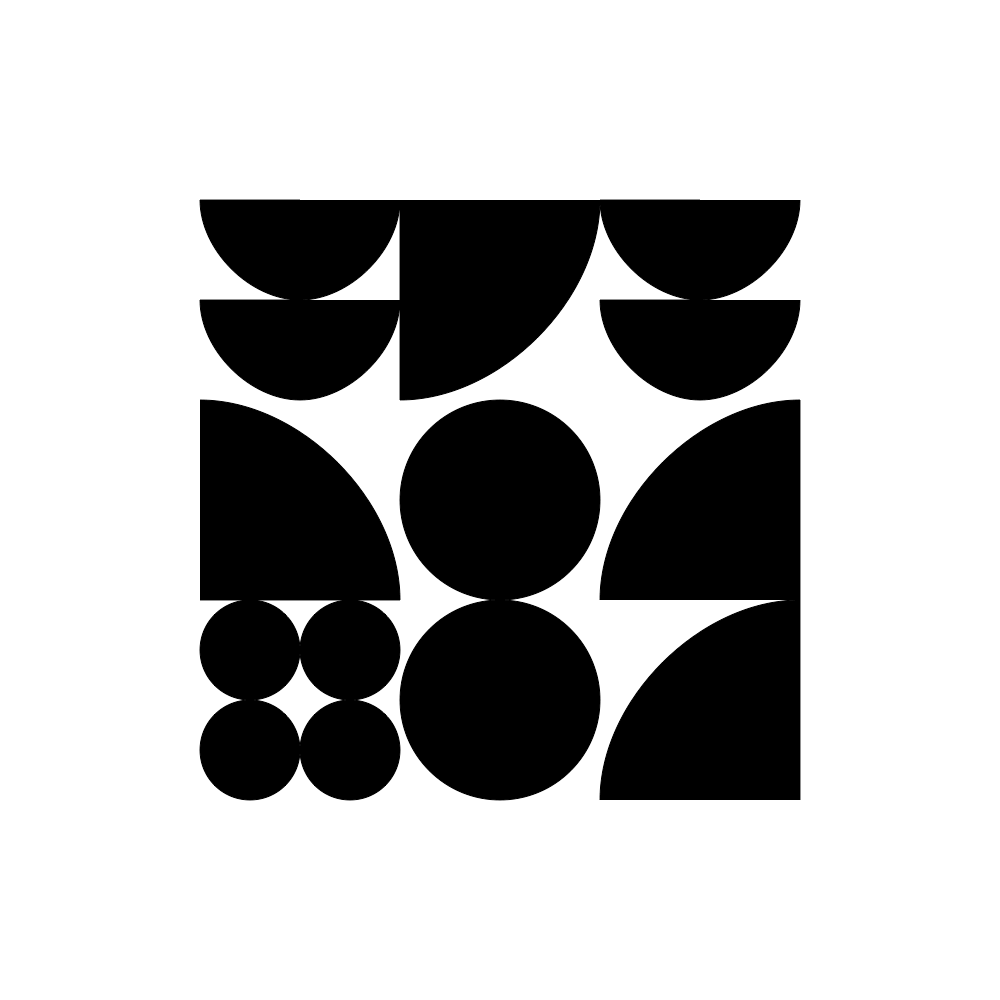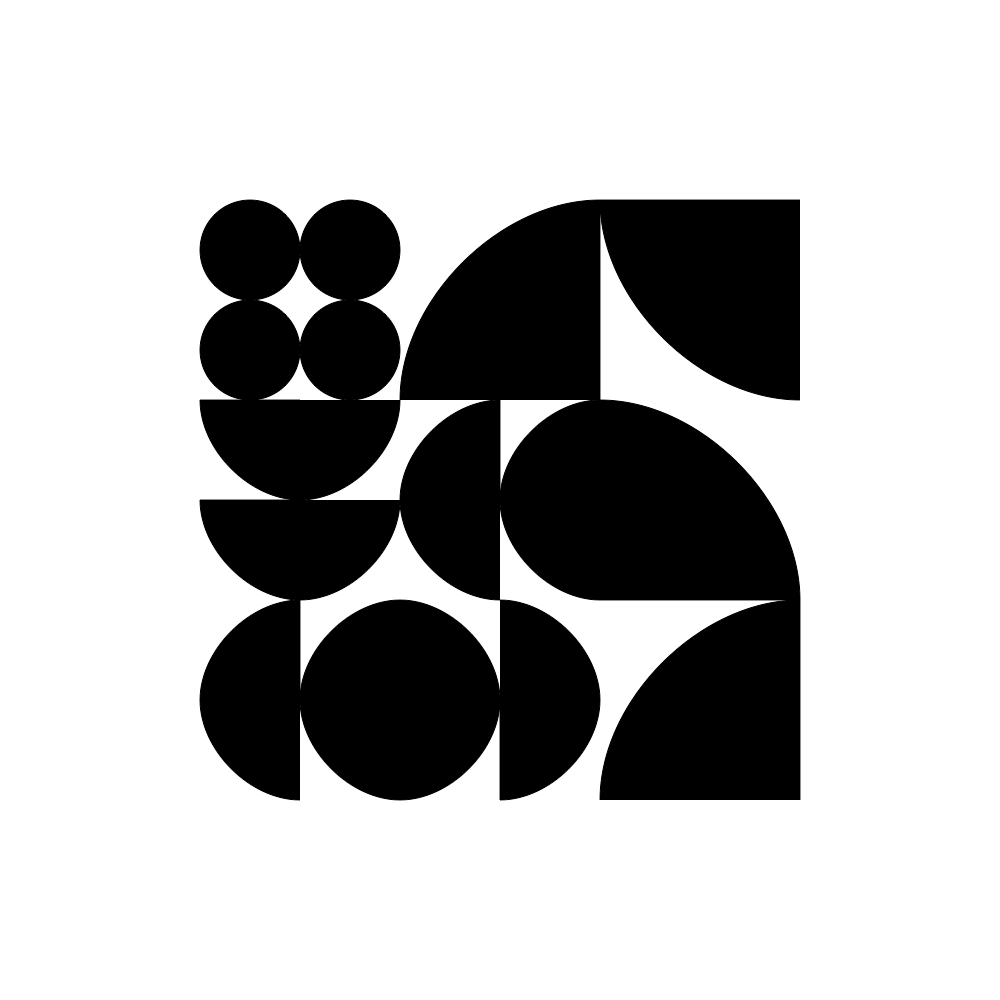
↑ all4PossibleShapes.py example script : here.
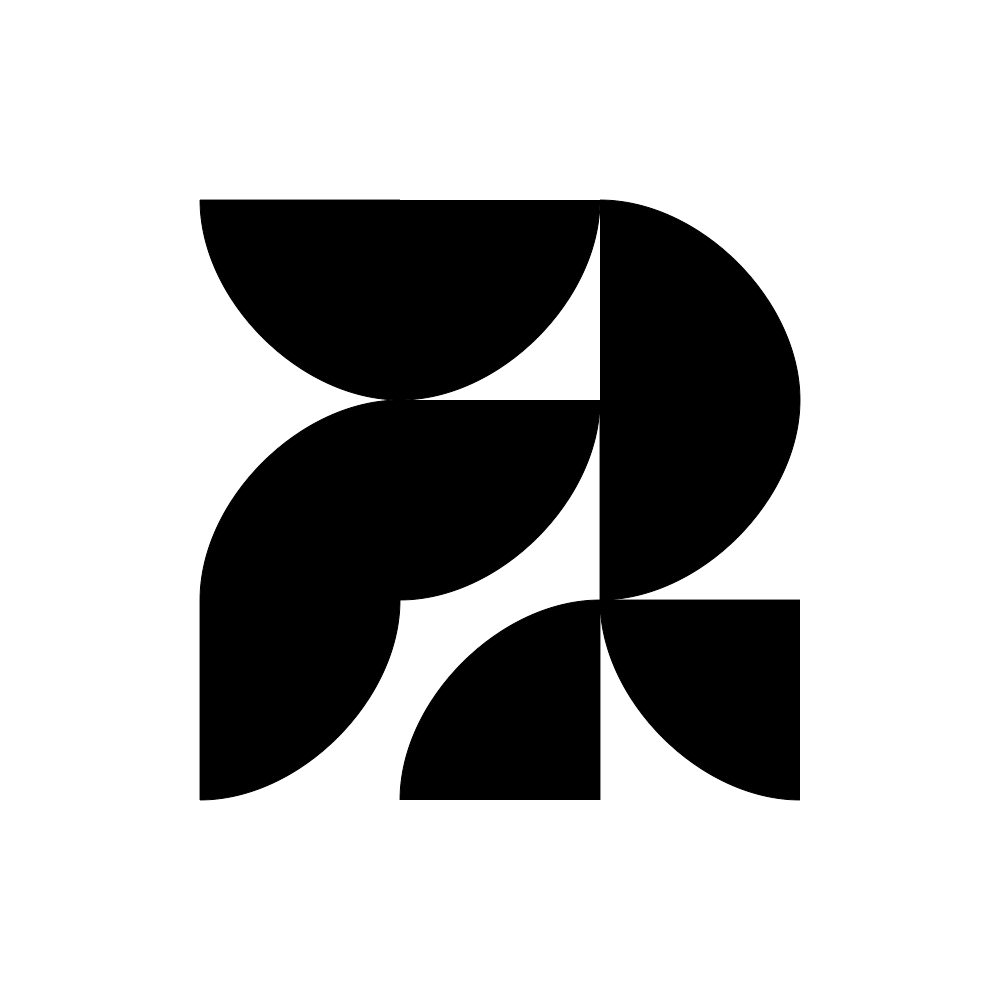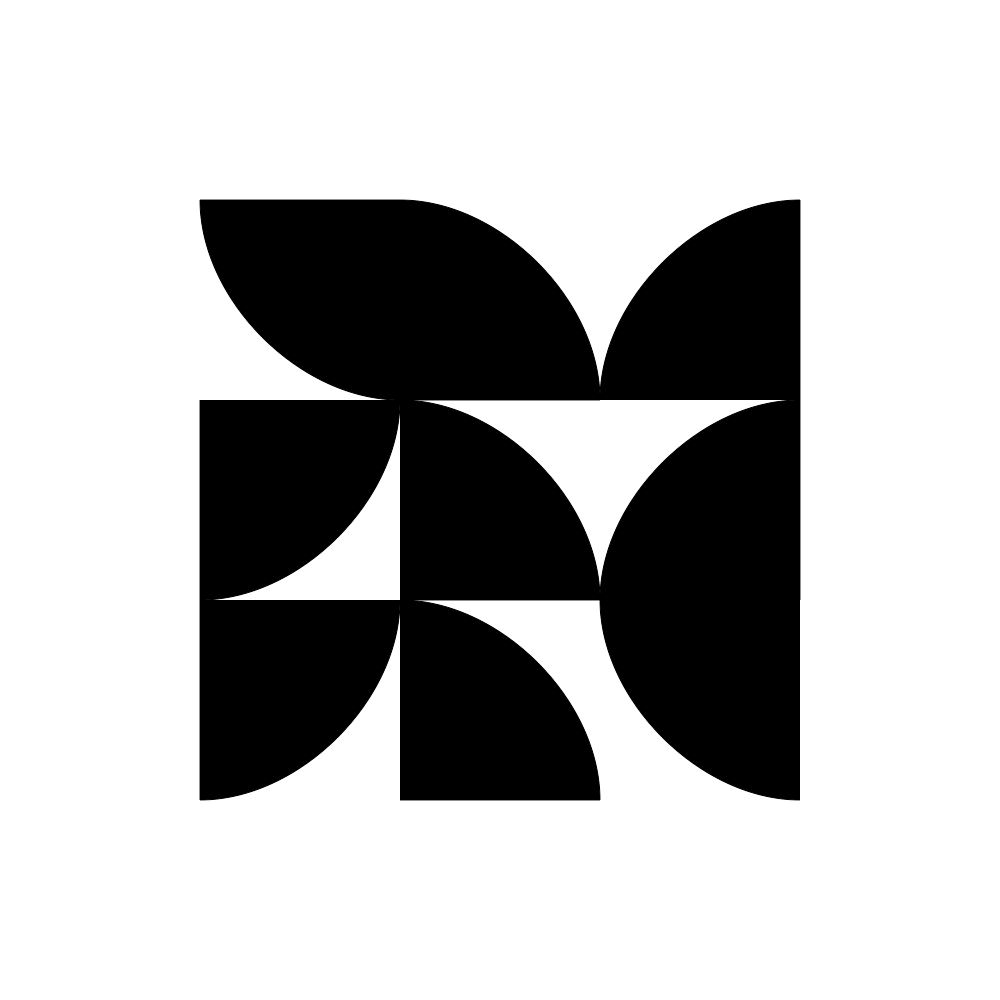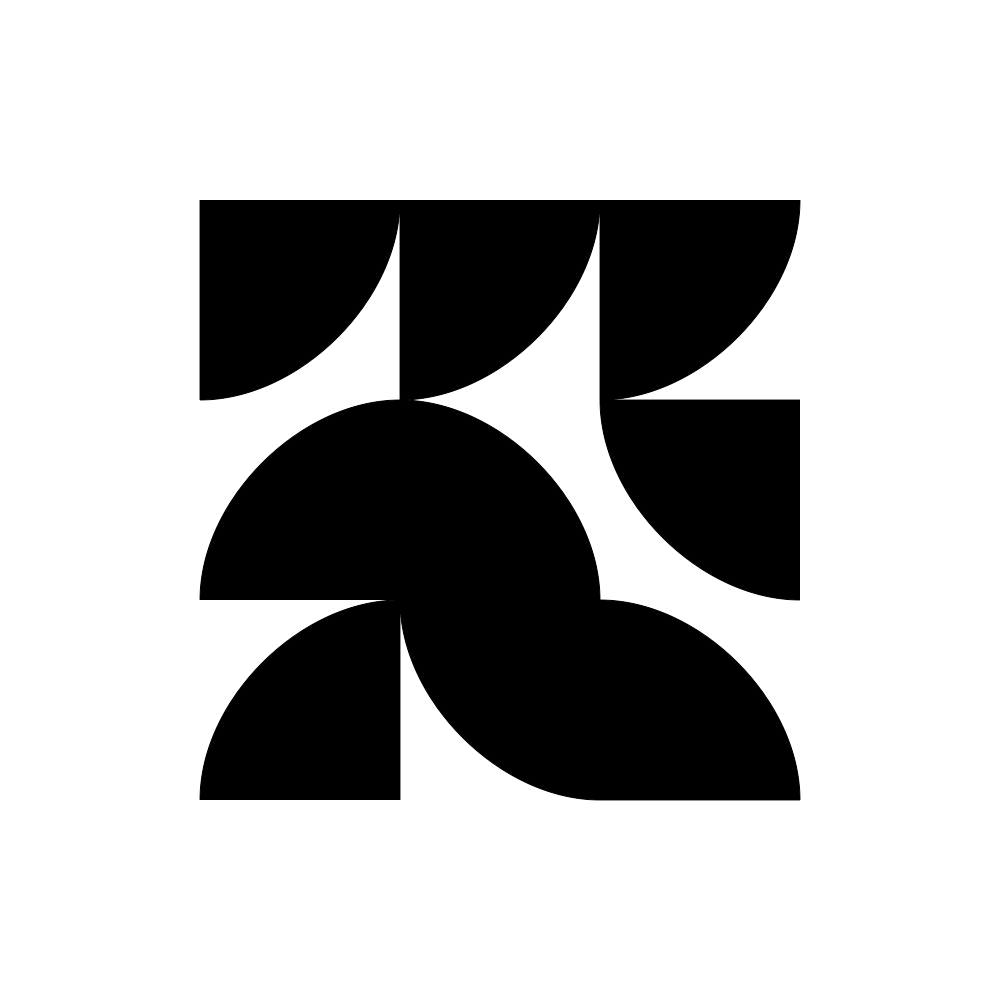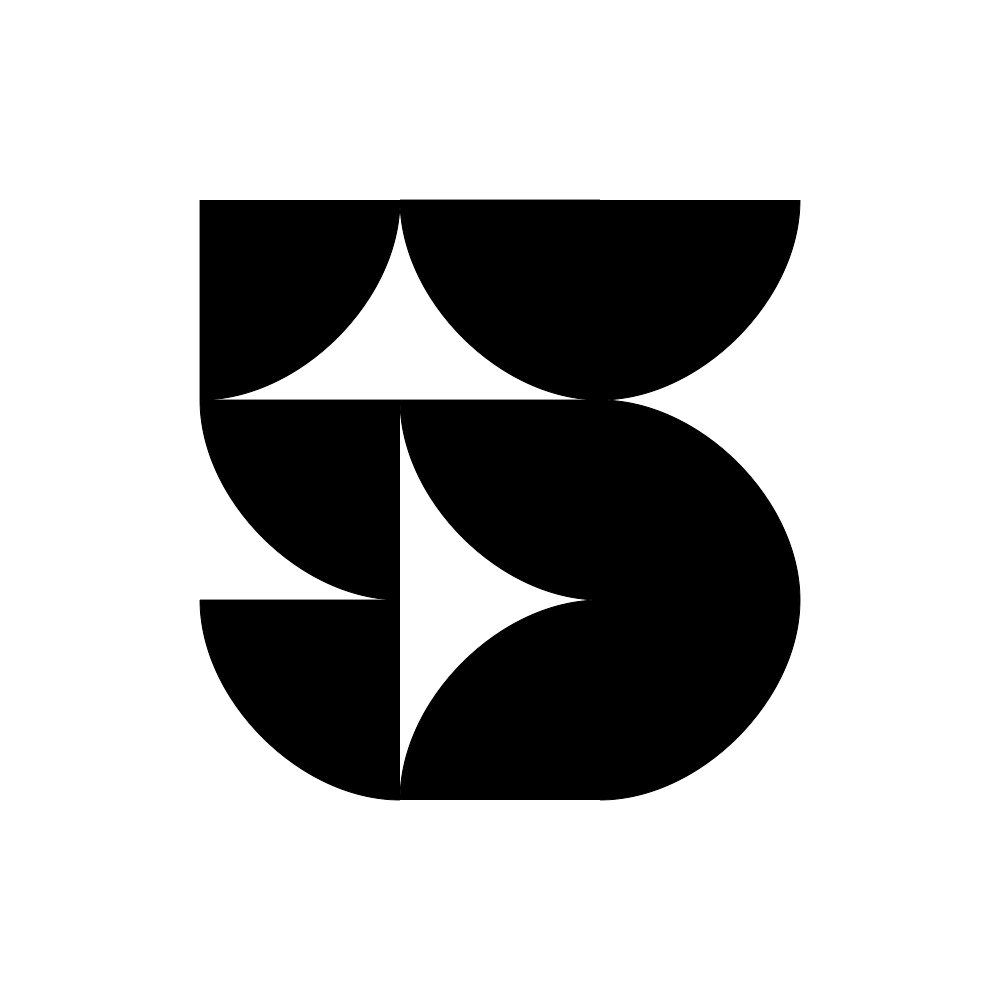
↑ allPossibleArcs.py example script : here.